| Copyright © 2003-2013 гг. Миргородский Александр Илларионович. |
Задача Диофанта и теорема Ферма
I. Задача Диофанта
В 1979 году мне удалось приобрести книгу в русском переводе "Творцы математики" известного американского историка математики Эрика Темпла Белла, изданную в США в 1937 году (Книгу в формате djvu можно скачать здесь ). . В книге один из её очерков посвящён Пьеру Ферма как королю любителей математики. По утверждению Э.Т. Белла, Ферма имел привычку, читая "Арифметику" Диофанта Александрийского и размышляя над её задачами, записывать на полях книги результаты своих размышлений в виде кратких замечаний. На полях второй книги "Арифметики", комментируя восьмую задачу Диофанта, Ферма написал:
"Наоборот, невозможно разложить ни куб на два куба, ни биквадрат на два биквадрата, и, вообще, никакую степень, большую квадрата на две степени с тем же показателем. Я открыл этому поистине чудесное доказательство, но эти поля для него слишком малы" /Э.Т.Белл «Творцы математики». М.,1979, стр.69 /.
Комментарий к задаче Диофанта, когда он был обнародован после смерти Ферма, получил название великой теоремы Ферма. В такой формулировке мне до этого времени она не была известна.
Размышления над примечанием Ферма к задаче Диофанта и размышления над задачей и её уравнением меня привели к предположению, что Ферма не написал условия теоремы и написал лишь её заключение, которое без её условия доказать невозможно в принципе. Условие теоремы определяет как её заключение, так и метод доказательства. По-моему, теорема Ферма такова:
" Если уравнение
| a 2 = x 2 + y 2 | (1) |
имеет бесконечное множество решений на множестве всех троек пифагоровых чисел, то, наоборот, уравнение
| x n + y n = z n, где n > 2 | (2) |
не имеет решений на множестве целых положительных чисел. "
.После Ферма его комментарий к задаче Диофанта не только принял форму уравнения (2). Гораздо важнее и существенно то, что оно оказалось лишённым необходимой связи с уравнением (1) и принятым одновремённо за условие и заключение великой теоремы Ферма. Других причин многолетних безуспешных поисков, я предположил, что Пьер Ферма не написал условия теоремы, а написал лишь её заключение, которое без условия теоремы доказать невозможно. Иной причины многолетних безуспешных поисков доказательства уравнения (2) я не нашёл. Включение уравнения (1) в великую теорему Ферма в качестве её условия не открывало путь к успешному поиску доказательства уравнения (2), а требовало в первую очередь детального исследования решений уравнения (1) на множестве всех троек пифагоровых чисел.
Историк математики Э.Т. Белл принимает восьмую задачу Диофанта в форме уравнения (1), в котором квадраты двух переменных x 2 и y 2 слагаются в a 2, поскольку мы читаем слева направо. Математики древних народов читали и писали справа налево и при жизни Диофанта могли рассматривать данное уравнение с противоположной стороны:
| a 2 = x 2 + y 2 | (3) |
Любое решение уравнения (3) представляет собой ( a, x, y ) тройка пифагоровых чисел. Каждая тройка пифагоровых чисел привязана к своему определённому натуральному числу, которое является и её индивидуальным порядковым номером. Между тройкой пифагоровых чисел и её номером, присутствующим в натуральном ряду чисел, существует взаимно однозначное соответствие.
Так, если дан индивидуальный номер, то по трём формулам можно определить числа тройки (a, x, y), а если дана тройка пифагоровых чисел, то можно по тем же формулам определить её индивидуальный номер.
Нечетное натуральное число N = 2k + 1 . К нему "привязана" тройка пифагоровых чисел. Числа тройки определяются по формулам:
| k = 1, 2, 3, ... | N = 3, k = 1 | ( y = 3, x = 4, a = 5 ) | |||
| y = N = 2k + 1 | N =5, k = 2 | ( y = 5, x = 12, a = 13 ) | |||
|
N = 7, k = 3 | ( y = 7, x = 24, a = 25 ) | |||
|
N = 9, k = 4 | ( y = 9, x = 40, a = 41 ) | |||
| N = 11, k = 5 | ( y = 11, x = 60, a = 61 ) | ||||
| и т. д. |
Чётное число N = 2k. К нему "привязана" тройка пифагоровых чисел. ( a, x, y ), её числа определяются по формулам:
| N = 2 k, | k = 2, 3, 4, ... | |
| y = 4 k | N = 4, k = 2 | ( y = 8, x = 15, a = 17 ) |
| x = 4 k 2 - 1 | N = 6, k = 3 | ( y = 12, x = 35, a = 37 ) |
| N = 8, k = 4 | ( y = 16, x = 63, a = 65 ) | |
| a = 4 k 2 + 1 | N = 10, k = 5 | ( y = 99, x = 99, a = 101 ) |
| и т. д. |
Кроме троек пифагоровых чисел, "привязанных" к своему индивидуальному номеру, по которому они определяются указанными формулами, существует бесконечное множество троек пифагоровых чисел, "свободных" от номеров, "безномерных", которые находятся по другим формулам. Например, тройки пифагоровых чисел ( y = 20, x = 21, a = 29 ), ( y = 33, x = 56, a = 65 ) и другие не имеют индивидуальных номеров и дополняют собой множество пифагоровых чисел, имеющих индивидуальные номера.
Если каждому натуральному числу N > 2 соответствует своя определенная тройка пифагоровых чисел, если их счетное множество объединить с множеством "безномерных" пифагоровых чисел, то объединённое множество пифагоровых чисел будет заключать в себе натуральный ряд чисел в качестве подмножества.
В уравнении (3) a 2 получает своё определение и выражение в форме суммы переменных x 2 и y 2 .
Произвольно взятый квадрат числа a 2 в процессе разложения на x 2 и y 2 не изменяет своего числового значения, доказывая свою независимость от числовых значений переменных x 2 и y 2 .
Изменение значений переменных x и y находится в подчинённом отношении к значению постоянной a. Они принимают значения, которые меньше значения a, и только те значения, при которых сумма их квадратов равна квадрату a. Другими словами, область допустимых значений переменных x и y определяется значением постоянной a : x < a, y < a.
Нахождение решений уравнения (3), равносильного уравнению (1), сводится:
По теореме Пифагора, площадь квадрата, построенного на гипотенузе a прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах x и y.
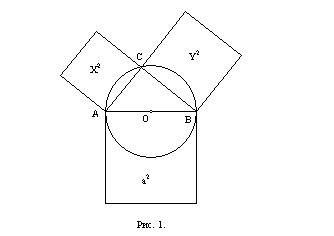 Между членами уравнения (3) и площадями квадратов, построенных на сторонах прямоугольного треугольника, существует взаимно однозначное соответствие. Можно себе представить, что тройки чисел уравнения (3) сбросили с себя форму натуральных чисел и приняли на себя геометрическую форму сторон и площадей квадратов.
Между членами уравнения (3) и площадями квадратов, построенных на сторонах прямоугольного треугольника, существует взаимно однозначное соответствие. Можно себе представить, что тройки чисел уравнения (3) сбросили с себя форму натуральных чисел и приняли на себя геометрическую форму сторон и площадей квадратов.
Из данного условия следует заключение: можно разложить площадь квадрата на площади двух квадратов.
Квадраты a 2 , x 2 и y 2 можно рассматривать в трёхмерном пространстве как квадратные основания трёх параллелепипедов одинаковой произвольной высоты h.
Умножим обе стороны уравнения (3) на целое число h. В результате получаем уравнение:
| a 2 h = x 2 h + y 2 h | (4) |
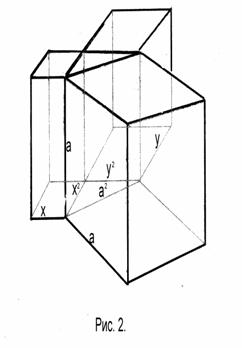 Уравнение (4) равносильно уравнению (3), так как все решения уравнения (3) являются решениями уравнения (4) и обратно. На левой стороне уравнения (4), произведение a2h можно рассматривать как объём параллелепипеда высотой h, построенного на квадрате гипотенузы a. Высота h может иметь значение любого натурального числа, так что верхнее основание параллелепипеда может оказаться выше облаков. (Рис.2)
Уравнение (4) равносильно уравнению (3), так как все решения уравнения (3) являются решениями уравнения (4) и обратно. На левой стороне уравнения (4), произведение a2h можно рассматривать как объём параллелепипеда высотой h, построенного на квадрате гипотенузы a. Высота h может иметь значение любого натурального числа, так что верхнее основание параллелепипеда может оказаться выше облаков. (Рис.2)
На правой стороне уравнения (4) произведение x2h можно рассматривать как объём параллелепипеда высотой h, построенного на квадрате, принадлежащем катету x. Произведение y2h можно рассматривать как объём параллелепипеда высотой h, построенного на квадрате, принадлежащем катету y. Площадь основания параллелепипеда левой стороны уравнения равна сумме площадей оснований параллелепипедов правой стороны уравнения.
При равенстве площади a2 сумме площадей x2 и y2 и при равенстве высот h трёх параллелепипедов объём параллелепипеда, построенного на квадрате, принадлежащем гипотенузе a, разлагается на объемы двух параллелепипедов, построенных на квадратах, принадлежащих катетам x и y. Следовательно, уравнение (4) показывает, что объём параллелепипеда a2h его левой стороны разлагается на объёмы x2h и y2h двух параллелепипедов его правой стороны. Высота h параллепипедов может быть равна любому целому положительному числу, включая: h = a, при котором уравнение (4) обращается в равносильное уравнение.
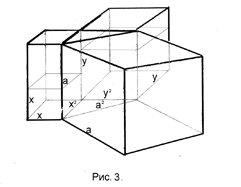
| a 3 = x 2 a + x 2 a | (5) |
Из уравнения (5) следует: куб a разлагается на два параллелепипеда x 2a и y 2a . Оно является равносильным уравнению (1), которое было принято за условие великой теоремы Ферма, нуждающееся в детальном исследовании и освоении всего относящегося к нему материала. Теперь его исследование выполнено, существование бесконечного множества решений уравнения (5) и равносильного ему уравнения (1) на множестве всех троек пифагоровых чисел установлено окончательно и не может вызывать сомнения. Появилась реальная возможность начать поиск доказательства заключения (2) великой теоремы Ферма, основанием которого является принятое мной её условие (1).
II. Доказательство великой теоремы Ферма
Сравним комментарий Ферма к задаче Диофанта с современной формулировкой великой теоремы Ферма, имеющей вид уравнения.
«Уравнение
Комментарий находится с задачей в логической связи, аналогичной логической связи сказуемого с подлежащим. То, что утверждается задачей Диофанта, наоборот утверждается комментарием Ферма.
Комментарий Ферма можно так трактовать: если квадратное уравнение с тремя неизвестными имеет бесконечное множество решений на множестве всех троек пифагоровых чисел, то, наоборот, уравнение с тремя неизвестными в степени, большей квадрата, не имеет решений в целых положительных числах.
В уравнении нет даже намека на его связь с задачей Диофанта. Его утверждение требует доказательства, но при нём нет условия, из которого следует, что оно не имеет решений в целых положительных числах.
Известные мне варианты доказательства уравнения сводятся к следующему алгоритму.
- Уравнение теоремы Ферма принимается за её заключение, в справедливости которого убеждаются при помощи доказательства.
- Это же уравнение называют исходным уравнением, из которого должно исходить его доказательство.
- Принимается предположение, противоположное тому, что утверждается уравнением, которое требуется доказать. Оно не должно противоречить исходному уравнению, а оно ему противоречит. Доказывать то, что принято без доказательства, и принимать без доказательства то, что требуется доказать, не имеет смысла.
- На основании принятого предположения выполняются абсолютно правильные математические операции и действия, чтобы доказать, что оно противоречит исходному уравнению и является ложным.
В результате образовалась тавтология: «Если уравнение не имеет решений в целых положительных числах, то оно не имеет решений в целых положительных числах».Доказательство тавтологии заведомо является неправильным и лишенным всякого смысла. Но её доказывают методом от противного.
Поэтому вот уже 370 лет доказательство уравнения великой теоремы Ферма остаётся неосуществимой мечтой специалистов и любителей математики.
Я принял уравнение за заключение теоремы, а восьмую задачу Диофанта и её уравнение - за условие теоремы.
"Если уравнение x 2 + y 2 = z 2 (1) имеет бесконечное множество решений на множестве всех троек пифагоровых чисел, то, наоборот, уравнение x n + y n = z n, где n > 2 (2) не имеет решений на множестве целых положительных чисел."
А) Всем известно, что уравнение (1) имеет бесконечное множество решений на множестве всех троек пифагоровых чисел. Докажем, что ни одна тройка пифагоровых чисел, являющаяся решением уравнения (1), не является решением уравнения (2).
На основании закона обратимости равенства, стороны уравнения (1) поменяем местами. Пифагоровы числа (z, х, у) могут быть истолкованы как длины сторон прямоугольного треугольника, а квадраты ( x 2, y 2, z 2) могут быть истолкованы как площади квадратов, построенных на его гипотенузе и катетах.
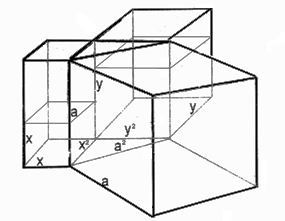
Площади квадратов уравнения (1) умножим на произвольную высоту h:
Уравнение (3) можно трактовать как равенство объема параллелепипеда сумме объёмов двух параллелепипедов.
Пусть высота трех параллелепипедов h = z:
Объем куба разложился на два объема двух параллелепипедов. Объём куба оставим без изменений, а высоту первого параллелепипед уменьшим до x и высоту второго параллелепипеда уменьшим до y. Объём куба больше суммы объёмов двух кубов:
На множестве троек пифагоровых чисел (х, у, z) при n = 3 не может быть ни одного решения уравнения (2). Следовательно, на множестве всех троек пифагоровых чисел невозможно куб разложить на два куба.
Пусть в уравнении (3) высота трёх параллелепипедов h = z 2:
Объем параллелепипеда разложился на сумму объёмов двух параллелепипедов.
Левую сторону уравнения (7) оставим без изменения. На правой его стороне высоту z 2 уменьшим до х в первом слагаемом и до у 2
во втором слагаемом.
Уравнение (7) обратилось в неравенство:
| z 4 > x 4 + y 4 | (7) |
На множестве троек пифагоровых чисел при n=4 не может быть ни одного решения уравнения (2). Следовательно, на множестве всех троек пифагоровых чисел невозможно биквадрат разложить на два биквадрата.
Пусть в уравнении (3) высоты параллелепипедов h = z n-2
| z n = x 2z n-2 + y 2z n-2 | (8) |
Объем параллелепипеда разложился на два объема двух параллелепипедов.
Левую сторону уравнения (8) оставим без изменения.
На правой стороне высоту z n-2 уменьшим до x n-2 в первом слагаемом и уменьшим до y n-2 во втором слагаемом. Уравнение (8) обращается в неравенство:
| z n > x n + y n | (9) |
На множестве троек пифагоровых чисел не может быть ни одного решения уравнения (2).
Следовательно, на множестве всех троек пифагоровых чисел при всех n > 2 уравнение (2) не имеет решений.
Получено "постине чудесное доказательство", но только для троек пифагоровых чисел. В этом заключается недостаток доказательства и причина отказа П. Ферма от него.
B) Докажем, что уравнение (2) не имеет решений на множестве троек непифагоровых чисел, представляющем сбой семейство произвольно взятой тройки пифагоровых чисел z = 13, x = 12, y = 5 и семейство произвольно взятой тройки целых положительных чисел z = 21, x = 19, y = 16
Обе тройки чисел являются членами своих семейств:
| (13, 12, 12); (13, 12,11);...; (13, 12, 5);...; (13,7, 1);...; (13,1, 1) | (10) | |
| (21, 20, 20); (21, 20, 19);...;(21, 19, 16);...;(21, 1, 1) | (11) |
Число членов семейства (10) и (11) равно половине произведения 13 на 12 и 21 на 20, т. е. 78 и 210.
В каждом члене семейства (10) присутствует z = 13 и переменные х и у, которые принимают значения целых чисел 13 > x > 0 , 13 > y > 0. Переменные последовательно убывают на 1
.В каждом члене семейства (11) присутствует z = 21 и переменные х и у, которые принимают значения целых чисел 21 > x >0, 21 > y > 0. Переменные последовательно убывают на 1.
Тройки чисел последовательности (10) и (11) можно представить в виде последовательности неравенств третьей степени:
| 133 < 12 3 + 12 3 ;13 3 < 12 3 + 11 3 ;...; 13 3 < 12 3 + 8 3; 13 3 > 12 3 + 7 3 ;...; 13 3 > 1 3 + 1 3 | ||
| 21 3 < 20 3 + 20 3 ; 21 3 < 20 3 + 19 3 ; ...; 21 3 < 19 3 + 14 3 ; 21 3 > 19 3 + 13 3 ;...; 21 3 > 1 3 + 13 |
и в виде неравенств четвертой степени:
| 13 4 < 12 4 + 12 4 ;...; 13 4 < 12 4 + 10 4 ; 13 4 > 12 4 + 9 4 ;...; 13 4 > 1 4 + 1 4 | ||
| 21 4 < 20 4 + 20 4 ; 21 4 < 20 4 + 19 4 ; ...; 21 4 < 19 4 + 16 4 ;…; 21 4 > 1 4 + 1 4 |
Правильность каждого неравенства удостоверяется возвышением чисел в третью и в четвертую степень.
Куб большего числа невозможно разложить на два куба меньших чисел. Он или меньше, или больше, суммы кубов двух меньших чисел.
Биквадрат большего числа невозможно разложить на два биквадрата меньших чисел. Он или меньше, или больше, суммы биквадратов меньших чисел.
С возрастанием показателя степени все неравенства, кроме левого крайнего неравенства, имеют одинаковый смысл:
| 13 8 < 12 8 + 12 8 ; 13 8 > 12 8 + 11 8 ;...; 13 8 > 12 8 + 5 8 ;...; 13 8 > 1 8 + 1 8 | ||
| 21 14 < 20 14 + 20 14 ; 21 14 > 20 14 + 19 14 ; ...; 21 14 > 19 14 + 16 14 ; ...; 21 14 > 1 14 + 1 14 |
При возрастании показателя степени еще на 1 все неравенства, включая и левые крайние неравенства, имеют одинаковый смысл:
| 13 9 > 12 9 + 12 9 ; > 12 9 + 11 9 ;…; > 12 9 + 5 9 ;…; > 1 9 + 1 9 | ||
| 21 15 > 20 15 + 20 15 ; 21 15 > 20 15 + 19 15 ; ...; 21 15 > 19 15 + 16 15 ; ...; 21 15 > 1 15 + 1 15 |
При дальнейшем возрастании показателя степени неравенств они все имеют одинаковый смысл: степень большего числа больше суммы степеней меньших двух чисел с тем же показателем:
| 13 n > 12 n + 12 n ; 13 n > 12 n + 11 n ;...; 13 n > 7 n + 4 n ;...; 13 n > 1 n + 1 n | (12) | |
| 21 n > 20 n + 20 n ; 21 n > 20 n + 19 n ;...; ;...; 21 n > 1 n + 1 n | (13) |
Левый крайний член последовательностей (12) (13) представляет собой наиболее слабое неравенство. Его правильность определяет правильность всех последующих неравенств последовательности (12) при n > 8 и последовательности (13) при n > 14.
Среди них не может быт ни одного равенства. Произвольно взятая тройка целых положительных чисел (21,19,16) не является решением уравнения (2) великой теоремы Ферма. Если произвольно взятая тройка целых положительных чисел не является решением уравнения, то уравнение не имеет решений на множестве целых положительных чисел, что и требовалось доказать.
С) В комментарии Ферма к задаче Диофанта утверждается, что невозможно разложить «вообще, никакую степень, большую квадрата, на две степени с тем же показателем».
Целую степень, большую квадрата, действительно невозможно разложить на две степени с тем же показателем. Нецелую степень, большую квадрата можно разложить на две степени с тем же показателем.
Любая произвольно взятая тройка целых положительных чисел (z, x, y) может принадлежать семейству, каждый член которого состоит из постоянного числа z и двух чисел, меньших z. Каждый член семейства может быть представлен в форме неравенства, а все полученные неравенства - в виде последовательности неравенств:
| zn < (z - 1)n + (z - 1)n; zn < (z - 1)n + (z - 2)n; …; zn > 1n + 1n | (14) |
Последовательность неравенств (14) начинается неравенствами, у которых левая сторона меньше правой стороны, а оканчивается неравенствами, у которых правая сторона меньше левой стороны. С возрастанием показателя степени n > 2 число неравенств правой стороны последовательности (14) увеличивается. При показателе степени n = k все неравенства левой стороны последовательности изменяют свой смысл и принимают смысл неравенств правой стороны неравенств последовательности (14). В результате возрастания показателя степени у всех неравенств левая сторона оказывается больше правой стороны:
| z k > (z-1) k + (z-1) k ; z k > (z-1) k + (z-2) k ;...; z k > 2 k + 1 k; z k > 1 k + 1 k | (15) |
При дальнейшем возрастании показателя степени n > k ни одно из неравенств не изменяет своего смысла и не обращается в равенство. На этом основании можно утверждать, что любая произвольно взятая тройка целых положительных чисел (z, x, y) при n > 2 , z > x, z > y не является решением уравнения большой теоремы Ферма.
В произвольно взятой тройке целых положительных чисел z может быть сколь угодно большим натуральным числом. Для всех натуральных чисел, которые не больше z, большая теорема Ферма доказана.
D) Каким бы ни было большим число z, в натуральном ряду чисел до него имеется большое, но конечное множество целых чисел, а после него – бесконечное множество целых чисел.
Докажем, что все бесконечное множество натуральных чисел, больших z, образуют тройки чисел, которые не являются решениями уравнения большой теоремы Ферма, например, произвольно взятая тройка целых положительных чисел (z + 1, x ,y), в которой z + 1 > x и z + 1 > y при всех значениях показателя степени n > 2 не является решением уравнения большой теоремы Ферма.
Произвольно взятая тройка целых положительных чисел (z + 1, x, y) может принадлежать семейству троек чисел, каждый член которого состоят из постоянного числа z + 1 и двух чисел х и у, принимающих различные значения, меньшие z + 1. Члены семейства могут быть представлены в форме неравенств, у которых постоянная левая сторона меньше, или больше, правой стороны. Неравенства можно упорядоченно расположить в виде последовательности неравенств:
| (z+1)n < zn + zn ; (z+1)n < zn + (z-1)n …; (z + 1)n > 1n + 1n | (16) |
С возрастанием показателя степени n > 2 число неравенств одинакового смысла правой стороны последовательности (16) увеличивается, а число неравенств её левой стороны одинакового, но противоположного смысла, уменьшается до нуля. Например, при показателе степени n = k левая сторона неравенств последовательности (16) исчезает, а в оставшейся её правой части все неравенства имеют одинаковый смысл:
| (z + 1)k > zk + zk; (z + 1)k > zk + (z – 1)k; …; (z + 1)k > 1k + 1k | (17) |
При дальнейшем возрастании показателя степени n > k до бесконечности ни одно из неравенств последовательности (17) не изменяет своего смысла и не обращается в равенство. В последовательности (16) неравенство, образованное из произвольно взятой тройки целых положительных чисел (z + 1, x, y), может находиться в её правой части в виде (z + 1) n > x n + y n или находиться в её левой части в виде (z + 1) n < x n + y n .
В любом случае тройка целых положительных чисел (z + 1, x, y) при n > 2 , z + 1 > x, z + 1 > y в последовательности (16) представляет собой неравенство и не может представлять собой равенства, т. е. не может представлять собой решения уравнения большой теоремы Ферма.
Легко и просто понять происхождение последовательности степенных неравенств (16), в которой последнее неравенство левой стороны и первое неравенство правой стороны являются неравенствами противоположного смысла. Наоборот, нелегко и непросто школьникам, старшекласснику и старшекласснице, понять, каким образом из последовательности неравенств (16) образуется последовательность неравенств (17), в которой все неравенства одинакового смысла.
В последовательности (16) увеличение целой степени неравенств на 1 единицу обращает последнее неравенство левой стороны в первое неравенство противоположного смысла правой стороны. Таким образом, количество неравенств девой стороны последовательности уменьшается, а количество неравенств правой стороны увеличивается. Между последним и первым степенными неравенствами противоположного смысла в обязательном порядке находится степенное равенство. Его степень не может быть целым числом, так как между двумя последовательными натуральными числами находятся только нецелые числа. Степенное равенство нецелой степени, по условию теоремы, не может считаться решением уравнения (1).
Если в последовательности (16) продолжать увеличение степени на 1 единицу, то последнее неравенство её левой стороны обратится в первое неравенство противоположного смысла правой стороны. В результате не останется ни одного неравенства левой стороны и останутся только неравенства правой стороны, которые представят собой последовательность усиливающихся степенных неравенств (17). Дальнейшее увеличение их целой степени на 1 единицу лишь усиливает её степенные неравенства и категорически исключает возможность появления равенства в целой степени.
Следовательно, вообще, никакую целую степень натурального числа (z+1) последовательности степенных неравенств (17) невозможно разложить на две целых степени с тем же показателем. Поэтому уравнение (1) не имеет решений на бесконечном множестве натуральных чисел, что и требовалось доказать.
Следовательно, большая теорема Ферма доказана во всей всеобщности:
- - в разделе А) для всех троек (z, x, y) пифагоровых чисел (открытое Ферма поистине чудесное доказательство),
- - в разделе В) для всех членов семейства любой тройки (z, x, y) пифагоровых чисел,
- - в разделе С) для всех троек чисел (z, x, y), не больших числа z,
- - в разделе D) для всех троек чисел (z, x, y) натурального ряда чисел.
Изменения внесены 05.09.2010 г. |
Какие теоремы можно и какие нельзя доказать от противного
В толковом словаре математических терминов дано определение доказательству от противного теоремы, противоположной обратной теореме.
«Доказательство от противного – метод доказательства теоремы (предложения), состоящий в том, что доказывают не саму теорему, а ей равносильную (эквивалентную), противоположную обратной (обратную противоположной) теорему. Доказательство от противного используют всякий раз, когда прямую теорему доказать трудно, а противоположную обратной легче. При доказательстве от противного заключение теоремы заменяется её отрицанием, и путём рассуждения приходят к отрицанию условия, т.е. к противоречию, к противному (противоположному тому, что дано; это приведение к абсурду и доказывает теорему».
Доказательство от противного очень часто применяется в математике. Доказательство от противного основано на законе исключённого третьего, заключающегося в том, что из двух высказываний (утверждений) А и А (отрицание А) одно из них истинно, а другое ложно». /Толковый словарь математических терминов: Пособие для учителей/О. В. Мантуров [и др.]; под ред. В. А. Диткина.- М.: Просвещение, 1965.- 539 с.: ил.-C.112/.
Не лучше было бы открыто заявить о том, что метод доказательства от противного не является математическим методом, хотя и используется в математике, что он является логическим методом и принадлежит логике. Допустимо ли утверждать, что доказательство от противного «используют всякий раз, когда прямую теорему доказать трудно», когда на самом деле его используют тогда, и только тогда, когда ему нет замены.
Заслуживает особого внимания и характеристика отношения друг к другу прямой и обратной ей теорем. «Обратная теорема для данной теоремы (или к данной теореме) - теорема, в которой условием является заключение, а заключением – условие данной теоремы. Данная теорема по отношению к обратной теореме называется прямой теоремой (исходной). В то же время обратная теорема к обратной теореме будет данной теоремой; поэтому прямая и обратная теоремы называются взаимно обратными. Если прямая (данная) теорема верна, то обратная теорема не всегда верна. Например, если четырёхугольник – ромб, то его диагонали взаимно перпендикулярны (прямая теорема). Если в четырёхугольнике диагонали взаимно перпендикулярны, то четырёхугольник есть ромб – это неверно, т. е. обратная теорема неверна». /Толковый словарь математических терминов: Пособие для учителей/О. В. Мантуров [и др.]; под ред. В. А. Диткина.- М.: Просвещение, 1965.- 539 с.: ил.-C.261 /.
Данная характеристика отношения прямой и обратной теорем не учитывает того, что условие прямой теоремы принимается как данное, без доказательства, так что его правильность не имеет гарантии. Условие обратной теоремы не принимается как данное, так как оно является заключением доказанной прямой теоремы. Его правильность засвидетельствована доказательством прямой теоремы. Это существенное логическое различие условий прямой и обратной теорем оказывается решающим в вопросе какие теоремы можно и какие нельзя доказать логическим методом от противного.
Допустим, что на примете имеется прямая теорема, которую доказать обычным математическим методом можно, но трудно. Сформулируем её в общем виде в краткой форме так: из А следует Е. Символ А имеет значение данного условия теоремы, принятого без доказательства. Символ Е имеет значение заключения теоремы, которое требуется доказать.
Доказывать прямую теорему будем от противного, логическим методом. Логическим методом доказывается теорема, которая имеет не математическое условие, а логическое условие. Его можно получить, если математическое условие теоремы из А следует Е, дополнить прямо противоположным условием из А не следует Е.
В результате получилось логическое противоречивое условие новой теоремы, заключающее в себе две части: из А следует Е и из А не следует Е. Полученное условие новой теоремы соответствует логическому закону исключённого третьего и соответствует доказательству теоремы методом от противного.
Согласно закону, одна часть противоречивого условия является ложной, другая его часть является истинной, а третье – исключено. Доказательство от противного имеет совей задачей и целью установить, именно какая часть из двух частей условия теоремы является ложной. Как только будет определена ложная часть условия, так будет установлено, что другая часть является истинной частью, а третье - исключено.
Согласно толковому словарю математических терминов, «доказательство есть рассуждение, в ходе которого устанавливается истинность или ложность какого-либо утверждения (суждения, высказывания, теоремы)». Доказательство от противного есть рассуждение, в ходе которого устанавливается ложность (абсурдность) заключения, вытекающего из ложного условия доказываемой теоремы.
Дано: из А следует Е и из А не следует Е.
Доказать: из А следует Е.
Доказательство: Логическое условие теоремы заключает в себе противоречие, которое требует своего разрешения. Противоречие условия должно найти своё разрешение в доказательстве и его результате. Результат оказывается ложным при безупречном и безошибочном рассуждении. Причиной ложного заключения при логически правильном рассуждении может быть только противоречивое условие: из А следует Е и из А не следует Е.
Нет и тени сомнения в том, что одна часть условия является ложной, а другая в этом случае является истинной. Обе части условия имеют одинаковое происхождение, приняты как данные, предположенные, одинаково возможные, одинаково допустимые и т. д. В ходе логического рассуждения не обнаружено ни одного логического признака, который отличал бы одну часть условия от другой. Поэтому в одной и той же мере может быть из А следует Е и может быть из А не следует Е. Утверждение из А следует Е может быть ложным, тогда утверждение из А не следует Е будет истинным. Утверждение из А не следует Е может быть ложным, тогда утверждение из А следует Е будет истинным.
Следовательно, прямую теорему методом от противного доказать невозможно.
Теперь эту же прямую теорему докажем обычным математическим методом.
Дано: А .
Доказать: из А следует Е.
Доказательство.
1. Из А следует Б (по ранее доказанной теореме).
2. Из Б следует В ( по ранее доказанной теореме)).
3. Из В следует Г ( по ранее доказанной теореме).
4. Из Г следует Д (по ранее доказанной теореме).
5. Из Д следует Е ( по ранее доказанной теореме).
На основании закона транзитивности, из А следует Е. Прямая теорема доказана обычным методом.
Пусть доказанная прямая теорема имеет правильную обратную теорему: из Е следует А.
Докажем её обычным математическим методом. Доказательство обратной теоремы можно выразить в символической форме в виде алгоритма математических операций.
Дано: Е
Доказать: из Е следует А.
Доказательство.
!. Из Е следует Д ( по ранее доказанной обратной теореме).
1. Из Д следует Г ( по ранее доказанной обратной теореме).
2. Из Г следует В (по ранее доказанной обратной теореме).
3. Из В не следует Б (обратная теорема неверна). Поэтому и из Б не следует А.
В данной ситуации продолжать математическое доказательство обратной теоремы не имеет смысла. Причина возникновения ситуации – логическая. Неверную обратную теорему ничем заменить невозможно. Следовательно, данную обратную теорему доказать обычным математическим методом невозможно. Вся надежда – на доказательство данной обратной теоремы методом от противного.
Чтобы её доказать методом от противного, требуется заменить её математическое условие логическим противоречивым условием, заключающим в себе по смыслу две части – ложную и истинную.
Обратная теорема утверждает: из Е не следует А. Её условие Е, из которое следует заключение А, является результатом доказательства прямой теоремы обычным математическим методом. Это условие необходимо сохранить и дополнить утверждением из Е следует А. В результате дополнения получается противоречивое условие новой обратной теоремы: из Е следует А и из Е не следует А. Исходя из этого логически противоречивого условия, обратную теорему можно доказать посредством правильного логического рассуждения только, и только, логическим методом от противного. В доказательстве от противного любые математические действия и операции подчинены логическим и поэтому в счёт не идут.
В первой части противоречивого утверждения из Е следует А условие Е было доказано доказательством прямой теоремы. Во второй его части из Е не следует А условие Е было предположено и принято без доказательства. Какое-то из них одно является ложным, а другое – истинным. Требуется доказать, какое из них является ложным.
Доказываем посредством правильного логического рассуждения и обнаруживаем, что его результатом является ложное, абсурдное заключение. Причиной ложного логического заключения является противоречивое логическое условие теоремы, заключающее в себе две части – ложную и истинную. Ложной частью может быть только утверждение из Е не следует А, в котором Е было принято без доказательства. Именно этим оно отличается от Е утверждения из Е следует А, которое доказано доказательством прямой теоремы.
Следовательно, истинным является утверждение: из Е следует А, что и требовалось доказать.
Вывод: логическим методом от противного доказывается только та обратная теорема, которая имеет доказанную математическим методом прямую теорему и которую математическим методом доказать невозможно.
Полученный вывод приобретает исключительное по важности значение в отношении к методу доказательства от противного великой теоремы Ферма. Подавляющее большинство попыток её доказать имеет в своей основе не обычный математический метод, а логический метод доказательства от противного. Доказательство большой теоремы Ферма Уайлса не является исключением.
Дмитрий Абраров в статье «Теорема Ферма: феномен доказательств Уайлса» опубликовал комментарий к доказательству большой теоремы Ферма Уайлсом. По Абрарову, Уайлс доказывает большую теорему Ферма с помощью замечательной находки немецкого математика Герхарда Фрея (р. 1944), связавшего потенциальное решение уравнения Ферма xn + yn = zn, где n > 2, с другим, совершенно непохожим на него, уравнением. Это новое уравнение задаётся специальной кривой (названной эллиптической кривой Фрея). Кривая Фрея задаётся уравнением совсем несложного вида:
y2 + x (x - an) (y + bn) = 0.
«А именно Фрей сопоставил всякому решению (a, b, c) уравнение Ферма, то есть числам, удовлетворяющим соотношению an + bn = cn, указанную выше кривую. В этом случае отсюда следовала бы великая теорема Ферма».( Цитата по: Абраров Д. «Теорема Ферма: феномен доказательств Уайлса»)
Другими словами, Герхард Фрей предположил, что уравнение большой теоремы Ферма xn + yn = zn, где n > 2, имеет решения в целых положительных числах. Этими же решения являются, по предположению Фрея, решениями его уравнения
y2 + x (x - an) (y + bn) = 0, которое задаётся его эллиптической кривой.
Эндрю Уайлс принял эту замечательную находку Фрея и с её помощью посредством математического метода доказал, что этой находки, то есть эллиптической кривой Фрея, не существует. Поэтому не существует уравнения и его решений, которые задаются несуществующей эллиптической кривой, Поэтому Уайлсу следовало бы принять вывод о том, что не существует уравнения большой теоремы Ферма и самой теоремы Ферма. Однако им принимается более скромное заключение том, что уравнение большой теоремы Ферма не имеет решений в целых положительных числах.
Неопровержимым фактом может являться то, что Уайлсом принято предположение, прямо противоположное по смыслу тому, что утверждается большой теоремой Ферма. Оно обязывает Уайлса доказывать большую теорему Ферма методом от противного. Последуем и мы его примеру и посмотрим, что из этого примера получается.
В большой теореме Ферма утверждается, что уравнение , xn + yn = zn, где n > 2, не имеет решений в целых положительных числах.
Согласно логическому методу доказательства от противного, это утверждение сохраняется, принимается как данное без доказательства, и затем дополняется противоположным по смыслу утверждением: уравнение xn + yn = zn, где n > 2, имеет решения в целых положительных числах.
Предположенное утверждение так же принимается как данное, без доказательства. Оба утверждения, рассматриваемые с точки зрения основных законов логики, являются одинаково допустимыми, равноправными и одинаково возможными. Посредством правильного рассуждения требуется установить, именно какое из них является ложным, чтобы затем установить, что другое утверждение является истинным.
Правильное рассуждение завершается ложным, абсурдным заключением, логической причиной которого может быть только противоречивое условие доказываемой теоремы, заключающее в себе две части прямо противоположного смысла. Они и явились логической причиной абсурдного заключения, результата доказательства от противного.
Однако в ходе логически правильного рассуждения не было обнаружено ни одного признака, по которому можно было бы установить, какое именно утверждение является ложным. Им может быть утверждение: уравнение xn + yn = zn, где n > 2, имеет решений в целых положительных числах. На этом же основании им может быть утверждение: уравнение xn + yn = zn, где n > 2, не имеет решений в целых положительных числах.
В итоге рассуждения вывод может быть только один: большую теорему Ферма методом от противного доказать невозможно.
В итоге рассуждения вывод может быть только один: большую теорему Ферма методом от противного доказать невозможно.
Было бы совсем другое дело, если бы большая теорема Ферма была обратной теоремой, которая имеет прямую теорему, доказанную обычным математическим методом. В этом случае её можно было доказать от противного. А так как она является прямой теоремой, то её доказательство должно иметь в своей основе не логический метод доказательства от противного, а обычный математический метод.
По словам Д. Абрарова, самый известный из современных российских математиков академик В. И. Арнольд на доказательство Уайлса отреагировал «активно скептически». Академик заявил: «это не настоящая математика – настоящая математика геометрична и сильна связями с физикой».( Цитата по: Абраров Д. «Теорема Ферма: феномен доказательств Уайлса»). Заявление академика выражает самую сущность нематематического доказательства Уайлса большой теоремы Ферма.
Методом от противного невозможно доказать ни того, что уравнение большой теоремы Ферма не имеет решений, ни того, что оно имеет решения. Ошибка Уайлса не математическая, а логическая - использование доказательства от противного там, где его использование не имеет смысла и большой теоремы Ферма не доказывает.
Не доказывается большая теорема Ферма и с помощью обычного математического метода, если в ней дано: уравнение xn + yn = zn, где n > 2, не имеет решений в целых положительных числах, и если в ней требуется доказать: уравнение xn + yn = zn, где n > 2, не имеет решений в целых положительных числах. В такой форме имеется не теорема, а тавтология, лишённая смысла.
Дополнено 27.07.2008 г. |
Примечание. Моё доказательство БТФ обсуждалось на одном из форумов. Один из участников Trotil, специалист в теории чисел, сделал следующее авторитетное заявление под названием: "Краткий пересказ того, что сделал Миргородский". Привожу его дословно:
"А. Он доказал, что если z2 = x2 + y , то zn > xn + y n. Это хорошо известный и вполне очевидный факт.
В. Он взял две тройки - пифагорову и не пифагорову и показал простым перебором, что для конкретного, определённого семейства троек (78 и 210 штук) БТФ выполняется (и только для него).
С. А затем автором опущен тот факт, что из < в последующей степени может оказаться = , а не только >. Простой контрпример - переход n = 1 в n = 2 в пифагоровой тройке.
D. Этот пункт ничего существенного в доказательство БТФ не вносит. Вывод: БТФ не доказана".
Рассмотрю его заключение по пунктам.
А. В нём доказана БТФ для всего бесконечного множества троек пифагоровых чисел. Доказана геометрическим методом, который, как я полагаю, мной не открыт, а переоткрыт. А открыт он был, как я полагаю, самим П. Ферма. Именно его мог иметь в виду Ферма, когда писал:
"Я открыл этому поистине чудесное доказательство, но эти поля для него слишком узки". Данное моё предположение основано на том, что в задаче Диофанта, против которой, на полях книги, писал Ферма, речь идёт о решениях диофантова уравнения, которыми являются тройки пифагоровых чисел.
Бесконечное множество троек пифагоровых чисел является решениями диофатова уравнения, а в теореме Ферма, наоборот, ни одно из решений не может быть решением уравнения теоремы Ферма. И к этому факту поистине чудесное доказательство Ферма имеет непосредственное отношение. Позже Ферма мог распространить свою теорему на множество всех натуральных чисел. На множестве всех натуральных чисел БТФ не относится к "множеству исключительно красивых теорем". Это - моё предположение, которое ни доказать, ни опровергнуть невозможно. Его можно и принимать и отвергать.
В. В данном пункте мной доказывается, что как семейство произвольно взятой пифагоровой тройки чисел, так и семейство произвольно взятой не пифагоровой тройки чисел БТФ выполняется, Это - необходимое, но недостаточное и промежуточное звено в моём доказательстве БТФ. Взятые мной примеры семейства тройки пифагоровых чисел и семейства тройки не пифагоровых чисел имеют значение конкретных примеров, предполагающих и не исключающих существование аналогичных других примеров.
Утверждение Trotil, что я "показал простым перебором, что для конкретного, определённого семейства троек (78 и 210 штук) БТФ выполняется (и только для него) лишено основания. Он не может опровергнуть того факта, что я с таким же успехом могу взять другие примеры пифагоровой и не пифагоровой тройки для получения конкретного определённого семейства одной и другой тройки.
Какую пару троек я ни взял бы, проверка их пригодности для решения задачи может быть осуществлена, на мой взгляд, только методом "простого перебора". Какой-то другой метод мне не известен и не требуется. Если он пришёлся не по вкусу Trotil,, то ему следовало бы предложить другой метод, чего он не делает. Не предлагая ничего взамен, осуждать "простой перебор", который в данном случае незаменим, некорректно.
С. Мною опущено = между < и < на основании того, что в доказательстве БТФ рассматривается уравнение z2 = x2 + y (1), в котором степень n > 2 - целое положительное число. Из равенства, находящегося между неравенствами следует обязательное рассмотрение уравнения (1) при нецелом значении степени n > 2. Trotil, считая обязательным рассмотрение равенства между неравенствами, фактически считает необходимым в доказательстве БТФ рассмотрение уравнения (1) при нецелом значении степени n > 2. Я это сделал для себя и обнаружил, что уравнение (1) при нецелом значении степени n > 2 имеет решением тройку чисел: z, (z-1), (z-1) при нецелом показателе степени:
| lq 2 | ||
| n = | ||
| lq z ⋅ lq (z-1) |
Если учесть, что Ферма написал: "невозможно разложить - вообще, никакую степень, большую квадрата, на две степени с тем же показателем", то следует заключить, что он ошибался и его теорема неверна. Этот результат был получен мною в 1979 г. Тогда было решено, что Ферма получил аналогичное заключение и поэтому отказался от обнародования теоремы. И я отказался от обнародования полученного результата. Но когда последовало в печати заявление о том, что Ферма соврал и что БТФ невозможно доказать элементарным методом, я выступил в защиту его чести и достоинства и опубликовал доказательство БТФ элементарным методом, без рассмотрения нецелой степени уравнения (1). Trotil заметил отсутствие равенства между двумя неравенствами, но без внимания к причине его отсутствия.
"Простой контрпример - переход n = 1 в n = 2 в пифагоровой тройке" он приводит вопреки условию БТФ n > 2.
D. В доказательстве БТФ данный пункт является совершенно необходимым и достаточным. В нём предыдущий пункт С (в котором БТФ доказана на конечном множестве натуральных чисел, не больших z), дополняется её доказательством на бесконечном множестве натуральных чисел. Этим самым исчерпывается весь набор троек, не удовлетворяющих решению уравнения (1). После этого, наконец, можно сказать, что БТФ доказана на всём бесконечном множестве натуральных чисел. Trotil, надо полагать, этого не понял, так как он утверждает, что "этот пункт ничего существенного в доказательство БТФ не вносит".
Кстати сказать, ученица 9-го класса СОШ №4 г. Черногорска республики Хакасия Анна Эверт, в письме от 7.01.2009 г. мне написала: "В интернете я нашла Ваше доказательство и полностью его поняла". Надеюсь, будут ещё и другие старшеклассники, которые поймут полностью моё доказательство БТФ.
Полностью понял моё доказательство БТФ Олег Анатольевич Рубетцаль, который дискутиравол с Trotil, как его оппонент. Станислав Климашевский написал: "Я восхощён простотой Вашего доказательства ВТФ..." Я считаю свое доказательство вполне удовлетворительным, но односторонним, верным только для целых показателей степени n>2. Мне казалось, что раскрытие факта неправильности БТФ для нецелых покозателей степени может уменьшить интерес к факту её правильности для целых показателей степени
Но обнародование вывода Trotil, специалиста в области теории чисел, несомненно, может значительно больше понизить интерес к моему доказательству правильности БТФ для целых показателей степени. Поэтому я был вынужден раскрыть факт её неправильности для нецелых показателей степени раньше запланированного мною времени.
Дополнено 09.09.2009 г. |
 Гостевая книга |
 |
| Web-дизайн © 2003-2013 гг. |
| Независимое научно-техническое издание "Научно - технический портал" |
| Увеличение посещаемости сайтов на 80-100%. Мгновенно. Бесплатно. |
| "СОЛО на клавиатуре" - эффективный курс обучения слепому десятипальцевому методу набора текста. |
|
|